Boolová algebra je dvojhodnotová logická algebra, ktorá používa disjunkciu (logický súčet), konjunkciu
(logický súčin) a negáciu (logická negácia) ako úplný súbor základných logických funkcií a slúži na
matematický opis zákonov a pravidiel výrokovej logiky, ktoré riešia vzťahy medzi pravdivými a nepravdivými výrokmi:
- pravdivý výrok – priradená hodnota logická 1
- nepravdivý výrok – priradená hodnota logická 0.
V Boolovej algebre sú definované 3 základné operácie, pomocou ktorých môžeme vyjadriť ľubovoľnú logickú operáciu: - logický súčet – disjunkcia
- logický súčin – konjunkcia
- logická negácia – negácia
Hodnoty závislej premennej Y, závislej od jednotlivých kombinácií nezávisle premenných A, B pre základné logické operácie znázorníme v pravdivostnej tabuľke. V ľavej časti tabuľky sú zapísané všetky kombinácie nezávislé premenných. V pravej časti tabuľky sú zapísané všetky stavy funkčných hodnôt výstupnej premennej Y.
Logický súčet
Logický súčet je operácia disjunkcie alebo zjednotenia a označuje sa znakom ש .V praxi sa často používa
algebraický zápis: Y = A + B
Pre operáciu logického súčtu je charakteristická spojka „alebo“ (anglicky „or“). Logický člen, ktorý realizuje
logický súčet, sa nazýva člen OR. Logický súčet sa rovná jednotke, keď aspoň jedna nezávisle premenná má hodnotu 1.
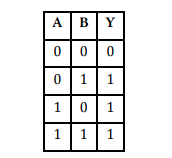
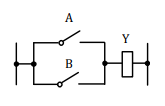
súčtu
Logický súčin
Logický súčin je operácia konjunkcie alebo prieniku, označuje sa znakom ר .V praxi sa často používa
algebraický zápis: Y = A . B
Pre operáciu logického súčinu je charakteristická spojka „aj“, „i“(anglicky „and“, „&”). Logický člen, ktorý
realizuje logický súčin, sa nazýva člen AND. Logický súčin sa rovná jednotke len vtedy, keď všetky nezávisle premenné majú hodnotu 1. Ak aspoň jedna vstupná premenná má hodnotu 0, výsledná hodnota sa rovná 0.
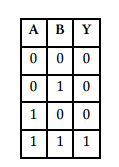
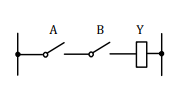
súčinu
Logická negácia
Logická negácia je operácia negácie, záporu. V p x ra i sa často používa algebraický zápis: Y = A negované
Pre operáciu logickej negácie je charakteristický zápis „nie“, („not“). Logický člen, ktorý realizuje logický
súčin, sa nazýva člen NOT, inventor alebo negátor. Logický negácia mení hodnotu nezávislej premennej na opačnú. Jej výsledok je rovný 1, ak A = 0 a opačne.
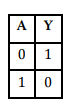
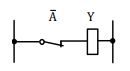
negácie
Pre Boolovu algebru platia nasledovné zákony a pravidlá:
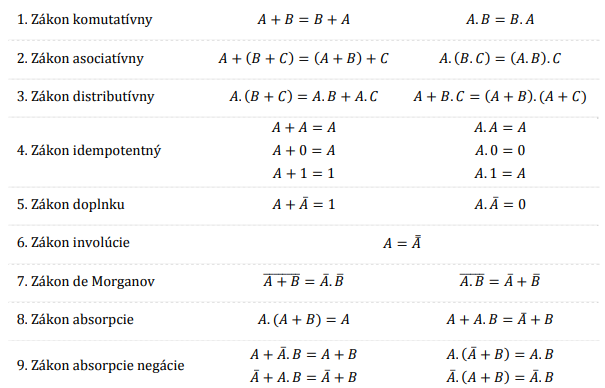
Všetky zákony a pravidlá možno dokázať zostavením pravdivostnej tabuľky ľavej a pravej strany rovnosti
a porovnaním.